The mystery of missing heritability: Genetic interactions create phantom heritability
Or Zuk, Eliana Hechter, Shamil R. Sunyaev, and Eric S. Lander
Human genetics has been haunted by the mystery of “missing heritability” of common traits. Although studies have discovered >1,200 variants associated with common diseases and traits, these variants typically appear to explain only a minority of the heritability. The proportion of heritability explained by a set of variants is the ratio of (i) the heritability due to these variants (numerator), estimated directly from their observed effects, to (ii) the total heritability (denominator), inferred indirectly from population data. The prevailing view has been that the explanation for missing heritability lies in the numerator—that is, in as-yet undiscovered variants. While many variants surely remain to be found, we show here that a substantial portion of missing heritability could arise from overestimation of the denominator, creating “phantom heritability.” Specifically, (i) estimates of total heritability implicitly assume the trait involves no genetic interactions (epistasis) among loci; (ii) this assumption is not justified, because models with interactions are also consistent with observable data; and (iii) under such models, the total heritability may be much smaller and thus the proportion of heritability explained much larger. For example, 80% of the currently missing heritability for Crohn's disease could be due to genetic interactions, if the disease involves interaction among three pathways. In short, missing heritability need not directly correspond to missing variants, because current estimates of total heritability may be significantly inflated by genetic interactions. Finally, we describe a method for estimating heritability from isolated populations that is not inflated by genetic interactions.
This new paper by Eric Lander and collaborators is attracting a fair amount of interest: gnxp , genetic inference , genomes unzipped. The paper is discussed at some length at the links above. I will just make a few comments.
1. The non-additive models analyzed in the paper require significant shared environment correlations to mask non-additivity and be consistent with data that (at face value) support additivity. See Table 7 in the Supplement. This level of environmental effect is, in the cases of height and g, probably excluded by adoption studies, although it may still be allowed for many disease traits. To put this another way, even after reading this paper I do not know of any models consistent with what is known about height and g that do not have a large additive component (e.g., of order 50 percent of total variance).
2. The criticisms in section 11 of Hill, Goddard, and Visscher (2008; also discussed previously here) are, to my mind, rather weak. To quote a string theorist friend: "It is nothing more than the calculus of words" ;-) In particular, I flat out disagree with the following (p.46 of the Supplement):
The problem with this reasoning is: As the population grows (and the typical locus tends toward monomorphism), typical traits involving typical loci become very boring! They not only have low interaction variance VAA, they also have very low total genetic variance VG. That is, the typical trait doesn't vary much in the population! In effect, Hill et al.'s theory thus actually describes what happens for rare traits caused by a few rare variants. Not surprisingly, interactions account for a small proportion of the variance for such traits.
[[ Nope, one could also take the rarity to zero and the number of causal variants to infinity keeping the population variance held fixed! This seems to be what happens in the real world with quantitative traits like height and g having thousands of causal variants, each of small effect. ]]
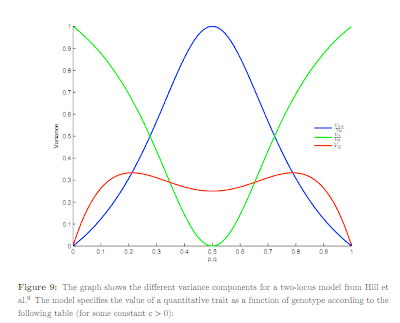
"Doesn't vary very much" is not well-defined: relative to what? What if the genetic variance in this limit is still much larger than the environmental component? Do height and IQ "vary very much" in human populations? Having only moderately rare variants (e.g., MAF = .1-.2), but many of them, is consistent with normally distributed population variation and small non-additive effects (.2 squared is 4 percent). Below is figure 9 from the Supplement -- click for larger version. As the frequency p approaches zero (or unity) the additive variance (green curve) dominates and the non-additive part becomes small (blue curve). Whether the total genetic variance (red curve) is big or small might be defined relative to the size of environmental effects, which are not shown. Note the green and blue curves are dimensionless ratios of variances, whereas the red curve ultimately (after multiplication by effect size) has real units like cm of height or IQ points.
The essence of Hill et al. is discussed in the earlier post (see comments).
Yes, one of the main points of the paper I cited is that one can have strong epistasis at the level of individual genes, but if variants are rare, the effect in a population will be linear.
"These two examples, the single locus and A x A model, illustrate what turns out to be the fundamental point in considering the impact of the gene frequency distribution. When an allele (say C) is rare, so most individuals have genotype Cc or cc, the allelic substitution or average effect of C vs. c accounts for essentially all the differences found in genotypic values; or in other words the linear regression of genotypic value on number of C genes accounts for the genotypic differences (see [3], p 117)." [p.5]
Note Added: For more on additivity vs epistasis, I suggest this talk by James Crow. Among other things he makes an evolutionary argument for why we should expect to find lots of additive variation at the population or individual level, despite the presence of lots of epistasis at the gene level. It is much more difficult for evolution to act on non-additive variance than on additive variance in a sexually reproducing species.

1 comment:
Personally, I favor epigenetic factors as a partial contributor to the missing heritability problem. Whatever the cause, it's certain that the heritability is some combination of biological factors that will be revealed in time.
Post a Comment